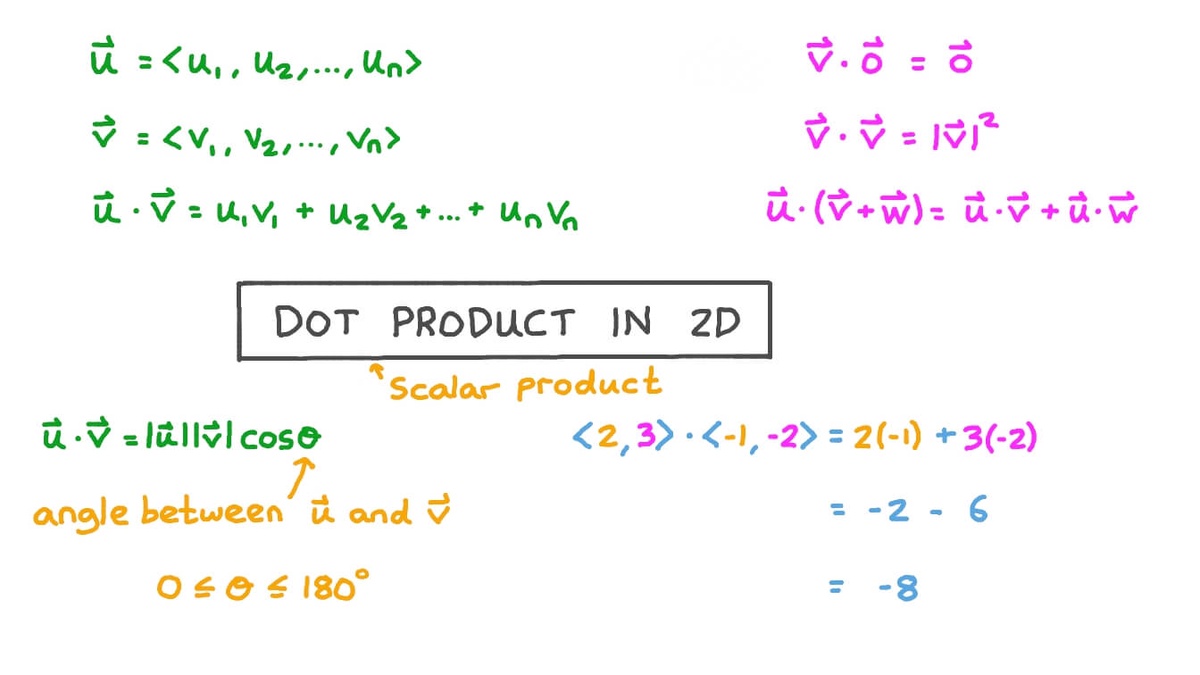
Calculus is a field that requires an understanding of many complex topics. One such topic is vector algebra, which deals with vectors and their components. One concept related to vectors is the dot product, or “scalar” product. Here we’ll take a look at what the dot product calculator is and how to calculate dot product for two given vectors.
What Is the Dot Product?
In mathematics, a dot product (also known as the scalar product) is an operation between two vectors in an inner product space that results in a single number. In Dot Product Calculator, the two vectors can be thought of as a measure of how similar they are: if the result is positive, then they point in the same direction; if negative, they point in opposite directions; if zero, then they are orthogonal (perpendicular).
How to Calculate the Dot Product of Two Vectors?
To calculate the dot product of two vectors, you need to first find the magnitudes (lengths) of each vector and then multiply them together. Then you need to find the angles between each vector and multiply that by their respective magnitudes. Finally, add up all these products and divide by 2 to get your final result. Here's an example: let's say we have two vectors A = [2, 3] and B = [4, 5]. First, calculate their magnitudes: |A| = √ (2² + 3²) = √13 ≈ 3.6 and |B| = √ (4² + 5²) = √41 ≈ 6.4. Then find the angle between them using cosine law θ = cos-1((A·B)/(|A||B|)) ≈ 0.5 radians. Multiply their magnitudes together |A||B| = 21.6. Finally, multiply this by θ (0.5) and divide by 2 to get your final result 21.6 * 0.5 /2 ≈ 10.8. This means that the dot product of vector A and B is 10.8!
Conclusion:
As you can see from this guide, calculating the dot product of two vectors can seem complicated at first glance but with some practice it becomes quite simple. Whether you’re learning calculus or just trying to brush up on your math skills, understanding to calculate in a dot product calculator will come in handy more often than you might expect.

No comments yet