When I was about 15, I had a week of ‘work experience’. Americans would call that an ‘internship’, but that’s not really right: work experience is a thing in British schools that basically just gets the older kids out of the way for a few days and palms them off on local businesses so the teachers can have a break.
I can’t actually remember the name of the company now, but anyway, they had a problem: they had recently scanned in a load of photos, all the history of the place, but those photos weren’t categorised: they just had hundreds, maybe a couple of thousands of pictures. all in one folder with arbitrary filenames. And the work experience kid got assigned the job of going through them all and writing descriptions. "Well, that’s boring", I thought, because of course I did. It was really dull. It’s the job you give the work experience kid, because they’re not disenchanted enough with the world yet.
So in between typing the descriptions, I figured I’d show off and write a system to search through them. It’d be like Yahoo, or that new Google thing that was starting to become popular. It’d look great. I’d look really smart. I didn’t know anything about how to build that, but with utterly unjustified confidence, I figured it couldn’t be that big a problem. And it wasn’t. Take the search word, loop through all the descriptions, count how many words match, then return all the matching results, sorted by the number of matches. And yeah. It worked fine. Until I got over about fifty photographs. At which point it started to get a little bit slow. And after a hundred, it started to get really slow. And I started to spend more time trying to fix it and less time actually doing my job. Actually, I mean, I wasn’t getting paid, so… Anyway, to explain why my code sucked: let’s talk about Big O Notation.
Whatever you’re coding, there are almost certainly many different ways to approach the problem. But even though all those approaches can end up with the same result, they may take vastly different amounts of time or memory to get there. And the best example of that is sorting. So we’ve got a bunch of different-sized blocks, we’ve got a list. What algorithms can we use to put our list in order?
Let’s start with something called bubble sort. Take the first two blocks and compare them. If the first one is longer than the second, swap them. If not, leave them where they are. Now compare the next two blocks. Same again. If they’re in the wrong order, swap them. If they’re not, leave them. And so on, and so on, until we get all the way to the end of the list. And at that point, we have moved the biggest block in the list to the very end. And that's all. And it's not very efficient, but it has now been done. So now we can go again from the start: we can compare, swap if we need to, compare, swap if we need to, compare, swap if we need to, and so on, and so on, and so on, and if we get all the way start-to-finish without moving a thing, then we know everything is sorted and we can stop. And if not: we go back to the start. And eventually, after many, many, many passes, congratulations, we have a sorted list!
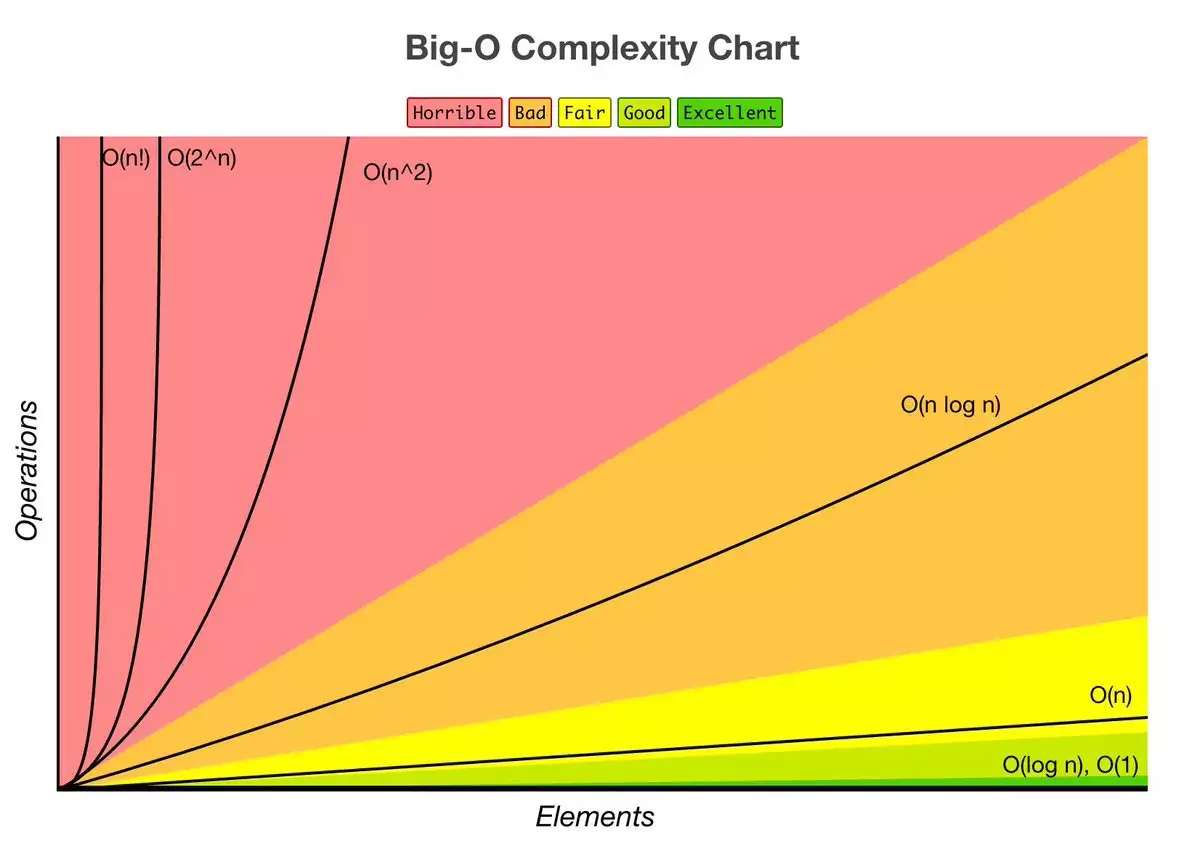
Bubble Sort, with each block “bubbling up”, is terrible. It has to check every block in the list on every pass, and in most cases it’ll have to pass through the list as many times as there are blocks on it. Ten blocks means ten operations, performed ten times. A hundred blocks means a hundred operations, performed a hundred times. The number of operations it has to perform goes up with the square of the number of blocks. Which means that it has a O(n²).
The foundations of Big O notation, plus that O symbol, were laid down towards the end of the 19th century by German mathematicians working in analytic number theory. But it was popularised in computer science by the great Donald Knuth in the 1970s. "Ka-nooth"? I should have checked that. Anyway. Big O distills an algorithm down to a single expression, which indicates how it performs as you add more blocks, more inputs of any kind. It lets you compare, roughly, approximately, in a big-picture sense, how slow an algorithm will get as you add more and more complexity.
n² means that the processing time goes up with the square of the number of inputs: double the number of inputs, and the run-time quadruples. The lowest Big O notation an algorithm can reasonably have is ‘constant’, O(1). That means that no matter how much stuff you throw at it, it’s going to return its answer in the same amount of time. And O(1) is usually something really simple, like “return the first item in the list”.
Some common algorithms have a O(n), or ‘linear’. This means that processing time goes up at a steady rate with the number of items. So if your code needs to go through a list and just do one thing to each item in it: that would be linear. Double the items, double the processing time.
So let’s try some other sorting algorithms. ‘Insertion sort’: start with the second item, compare it to the item before. If they’re the wrong way round, swap them. Now take the third item, and compare it to the one before: if they’re the wrong way round, swap them and then check again with the one before that. Basically, you keep moving each item in turn towards the start, checking as you go, until either you find something smaller and you know it's in the right place, or you reach the start of the list and you know it's the smallest. If you’ve got a hand of cards and you are putting them in numerical order, this is the algorithm you’re probably using without even thinking about it. And yes, that is usually faster than bubble sort. But crucially, its Big O notation is also O(n²). And this is a really important distinction to make: if two algorithms have the same Big O, it doesn’t mean they perform the same. It just means that if you draw the graphs of how they get worse with more inputs, those graphs have the same shape. For both bubble sort and insertion sort, if you double the number of items, it’ll quadruple the run time: but with insertion sort, that run time is usually shorter to begin with.
I’m not going to go into the details of every sorting algorithm, there are a lot of them, but there are two I want to flag up. The first is Quick Sort. Choose an item on the list and call it the ‘pivot’. Then go through the list, putting anything smaller than the pivot somewhere to its left, and anything larger somewhere to its right. Once that’s done, look at just the ones to the left of the pivot and you do the same, you choose a pivot and you split those. Repeat that divide-and-conquer all the way down. And then do the same to the other side of each of those pivot points, and work your way back up. And the worst-case Big O notation for this is still n². But the average performance on a random list is O(n log n). I'm not going into the mathematics, but suffice it to say that is a lot, lot better.
And then, on the other end of the scale, there is bogosort, which is designed as a joke. Bogosort is really simple: randomise the list. Is it sorted? Great! If it’s not, randomise again and keep going until it's sorted. The average performance there is O((n+1)!). Factorial. You can draw a graph of all the common Big O notations to compare them. But the important thing is: the Big O of whatever you’re coding is going to be mostly affected by the worst one of those that you have anywhere in it. If your code does ten operations that are linear and one that’s got a Big O of n²: well, your program is n² now. Remember it’s just an approximation, it’s a guide for humans to work out which algorithm is best to use. Despite being about computer science, it's a little bit fuzzy.
So what should I have done with my search system, back when I was a kid? Well, I could have used code that was already out there, realised that other people had done the work for me. That’s true. But ultimately what I should have done is what the client asked for: typed the descriptions into a word processor and saved it as a document. Because that was a better solution: they could have just searched it by pressing Control-F. Text doesn’t break down or need updating when an operating system gets upgraded. If they had new photos to add, anyone who knew how to type could update it. They could still open that document today. The big problem wasn’t that I used a bad algorithm: the big problem was that I was ignoring what my users actually needed because I wanted to show off how clever I thought I was. It’s important to think about how fast things will work, sure, but the best solution isn’t always the fastest, or the smartest. It’s the one that works for everyone, long-term.

No comments yet