Welcome to this series on Machine Learning Foundations. It's a course where you'll learn the fundamentals of building machine learning models using TensorFlow. The only thing that you'll need to know is a little bit of Python. So if you've tried to learn ML before and you were scared off by all the calculus and other math, well, this is the course for you. We'll start, in this episode, by talking about what machine learning actually is, as well as how it works.
So first of all, let's think a little bit about programming and what it looks like from a very high level. Perhaps you have to create some financial software where you write code that gets data and does something new with it. There's a popular analytic called a P/E ratio, which is called price to earnings. So code for that would look a little bit like this.  But please think in terms of the three things that I've labeled here. There's data, and there are rules that you'll write that act on that data. And that's where we programmers bring value, because those rules then provide answers.
But please think in terms of the three things that I've labeled here. There's data, and there are rules that you'll write that act on that data. And that's where we programmers bring value, because those rules then provide answers.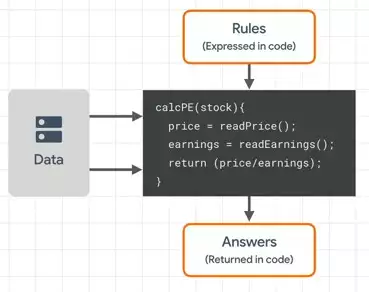 Another way you might program rules is like something like a game, where the game will respond to things that happen in the game world.
Another way you might program rules is like something like a game, where the game will respond to things that happen in the game world.
So maybe something like "Breakout," where once the ball hits the brick, the ball should bounce back, and the brick should vanish. So again, you have data, which is the location of the ball, the location of the bricks, et cetera. You have rules, which are the lines of code that you write. And you have answers-- how the game situation updates in response to these actions.
So again, you have data, which is the location of the ball, the location of the bricks, et cetera. You have rules, which are the lines of code that you write. And you have answers-- how the game situation updates in response to these actions.
So I like to summarize traditional programming like this using those terms. You have rules and data that come in, and you have answers that come out. And this is basically what we've all been making a living off of.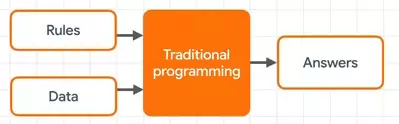
Traditional programming diagram
The ongoing machine learning revolution, from a programmer's perspective, is just a reorientation of this diagram.
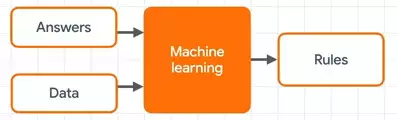
Machine learning diagram
So instead of us, as programmers, trying to figure out the rules that will give us the answers, what if we can feed in lots of answers along with the data and have a machine figure out what those rules are?
And that's really what machine learning is all about. Get lots of data, know what the answers are to that data -- and that's a process called labeling -- and then establish the rules that will match one to the other.
This might seem a little vague right now, so let's look at a scenario. Think about a device for activity recognition like a smartwatch. If you're creating one of these and you had sensors on it that provide data, such as the speed the person is moving at, what are the rules that you would write to give answers? Well, the answer, of course, is the activity that the person's performing.
For example, you might say that if the speed is less than a certain amount, the answer is that the person's walking. You could extend that, then, to say if it's greater than that amount, then the person's running. You've now detected two activities-- walking and running. It's a little naive, but hopefully it works just for illustration.
But what if you want to go further? Another fitness activity, for example, is biking. And you could extend your algorithm to understand biking like this. If the value's less than 4, they're walking. Otherwise, if it's less than 12, they're running. Otherwise they're biking. It's still kind of works, but what happens, then, if you want to detect golfing? Uh oh, indeed.
And not just golfing -- despite the naivete of this algorithm, it's easy to see where this is a really difficult scenario to implement with rules. Your speed will vary if you're going up or downhill, and your walking speed might be my running speed, and so on. Sometimes one cannot just simply figure out the rules to determine complex behavior like this.
So if we return to machine learning diagram and consider machine learning to be answers that data fed in and the rules get inferred from it, we could then change our activity recognition scenario.
So what if you had lots and lots of people wearing your sensor, and say that they're walking and that you've captured that data?  Similar for running, biking, and, yes, even golfing. What if you then looked at that data and had a way to figure out how to match the patterns to the label? You'd have a scenario that says this is what walking looks like, this is what running looks like, and so on. And that's really the core of machine learning -- having lots of data, having labels for that data, and then programming a computer to figure out what the distinguishing parts of the data are that fit to the labels.
Similar for running, biking, and, yes, even golfing. What if you then looked at that data and had a way to figure out how to match the patterns to the label? You'd have a scenario that says this is what walking looks like, this is what running looks like, and so on. And that's really the core of machine learning -- having lots of data, having labels for that data, and then programming a computer to figure out what the distinguishing parts of the data are that fit to the labels.
That was just a hypothetical scenario, but the same concept can apply to things like computer vision and natural language processing. And you'll learn those techniques throughout this course.
So let's start with a very simple scenario, and it's what I consider to be the hello world of machine learning. Take a look at these numbers.  There's a pattern that connects them. There's a relationship between the x and y that holds for each x, y pairing. So when x is minus 1, y is minus 3. And when x = 1, y = 1, et cetera. Can you see what the pattern is?
There's a pattern that connects them. There's a relationship between the x and y that holds for each x, y pairing. So when x is minus 1, y is minus 3. And when x = 1, y = 1, et cetera. Can you see what the pattern is?
The relationship here is that every y is 2 times the corresponding x - 1. Yes, I know we said we wouldn't do a lot of math, but I hope you're OK with this exception.
If you've got the answer, well, how did you get it? For me, I saw that y increased by 2 when x increased by 1, so I guessed that it was y equals 2x plus or minus something. I then took a guess that it might be -1, because when x = 0, the answer was -1. I looked back over all of the other numbers, and I found that that relationship worked. That's almost exactly how a neural network does it too.
So let's explore this in code. So here's an example of a TensorFlow app that will figure out that relationship for us.
model = keras.Sequential([keras.layers.Dense(units=1, input_shape=[1])]) model.compile(optimizer='sgd', loss='mean_squared_error') xs = np.array([-1.0, 0.0, 1.0, 2.0, 3.0, 4.0], dtype=float) ys = np.array([-2.0, 1.0, 4.0, 7.0, 10.0, 13.0], dtype=float) model.fit(xs, ys, epochs=500) print(model.predict([10.0]))
I know there's a whole lot of new concepts in here, so I'm going to unpack them one by one.
model = keras.Sequential([keras.layers.Dense(units=1, input_shape=[1])])
This is probably the most mysterious of the bunch, so let's explain it visually. You know how you often see pictures of neural networks that look a little like this?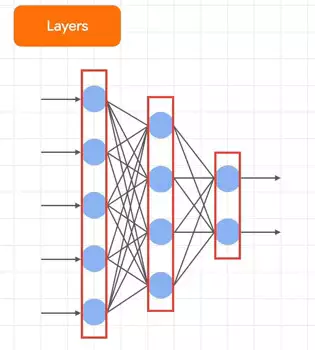 Each of the columns in the red boxes here are called layers, and each of the blue blobs are neurons. Every neuron is connected to every other neuron, and that's called a dense layer because of the dense connectivity between them. You define these kinds of neural networks using code. So let's look back at our code and see what we've defined.
Each of the columns in the red boxes here are called layers, and each of the blue blobs are neurons. Every neuron is connected to every other neuron, and that's called a dense layer because of the dense connectivity between them. You define these kinds of neural networks using code. So let's look back at our code and see what we've defined.
The first part of the line says that it's a keras.Sequential. Keras is a framework within TensorFlow for making the definition of training and using ML models easy. I'll be using it extensively in this course. The name sequential basically tells us that we're going to define a sequence of layers. In the diagram earlier, we had three layers. Well, how many layers do you think are in the network that we're defining in the code here? There's only one, because we only have one line of code within the sequential. Do you notice what type of layer it is? It's a dense, which is the simplest layer type there is with basic neurons in it. Later you'll learn more about sophisticated neuron types, but those in a dense are pretty basic.
What does our dense look like? Well, that's visible within the dense parameters. And we say we have only one unit, or one neuron in this layer. And we only have one layer. The input_shape parameter tells us the shape of the data that we'll train our layer on, and it's just one value. So our neural network will look like this. 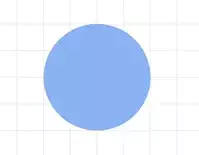 And that's the simplest neural network you can get-- one layer, one neuron. And what the neuron can do is learn to match data to labels. So let's see how this one will do it by returning to our code.
And that's the simplest neural network you can get-- one layer, one neuron. And what the neuron can do is learn to match data to labels. So let's see how this one will do it by returning to our code.
model.compile(optimizer='sgd', loss='mean_squared_error')
The core of how a network learns is in these two parameters-- the optimizer function and the loss function. Here's where all the math in machine learning comes from. Let me explain what they do.
The idea is that the neural network has no idea of the relationship between the data and the labels, so it has to make a guess. It then looks at the data and evaluates the guess. The loss function is a way of measuring how good or how bad that guess is. The results of this are used by the optimizer to make another guess. That guess is then measured using the loss function again, with the logic being that an optimizer can improve the guess. This data is passed back to the optimizer to get another guess, and so on. This is the process of training a neural network. In our code, we're going to be doing that loop-- making a guess, measuring its effectiveness with the loss function, optimizing to get another guess, and repeating -- 500 times. There's some complex math going on to measure the loss and optimize for a new guess, but we're not going to dwell on that for now.
The loss function here is called mean_squared_error, and the optimizer is sgd, which stands for stochastic gradient descent. We'll compile the model using them.
Next up, we're going to define our data.
xs = np.array([-1.0, 0.0, 1.0, 2.0, 3.0, 4.0], dtype=float) ys = np.array([-2.0, 1.0, 4.0, 7.0, 10.0, 13.0], dtype=float)
The NP stands for NumPy -- a Python library that makes handling data a lot easier, and which you'll see a lot of when you're using machine learning. We'll call our data x's, and we'll call our labels y's.
Next is where we do the learning.
model.fit(xs, ys, epochs=500)
We tell the model to fit the x's to the y's and do the loop that we spoke about earlier 500 times -- or 500 epochs. At the end of this, the rough guess that the neuron makes at the beginning will hopefully be refined into a good model that figured out the relationship between our x's and our y's.
Once the model is done training, you can then predict values using it.
print(model.predict([10.0]))
So given what we learned about x and y and that the relationship between them was y = 2x - 1, what do you think the answer to predicting 10.0 will be?
You might have thought that it would be 19 and you'll be very close to being right. But it won't be exactly 19 for a few reasons -- most notably the fact that this model is trained on only six points of data, and that for those six points of data, the relationship is linear. That is, y = 2x - 1. But there's no guarantee that that would be the case for other points. The data could skew off in other directions, and the neuron has no idea if that's the case or not, because it's only been trained on this limited data.
That being said, the probability that it's a straight line is very high, so the neuron factors that into its learning, and when asked to predict, it will give you a number very close to 19, because the probability is very high that the value for y when x is 10 is 19.
It's an important lesson to remember. Neural networks deal in probability. They'll give you a likelihood that an answer is correct, and you'll often have to deal with processing that likelihood.
So if we go back to traditional programming for a second, you might write a function like this and it would work.
getResult(x) {
return (2*x) - 1;
}
y = getResult(x);
But it would only ever return 2*x - 1, because it's hardcoded to do so. You could generalize the function like this
getResult(x, p1, p2) {
return (p1*x) - p2;
}
y = getResult(x, 2, -1);
where you pass in the parameters 2 and -1, and now the function will return 2x - 1, and if you wanted to use other values you could do so.
A neuron sort of works like this, where it has the parameters instead of hardcoded values, but it learns those parameters from the data over time. As a result, it's a general function that learns how to behave. And this is what leads to the term "machine learning." Our neurons are learning the parameters that will give the desired results, with a view to those results then working in the future with other data.


No comments yet